LINEAR PROGRAMMING

LINEAR PROGAMMING

A.      KONSEP DASAR LINEAR PROGRAMMING

Konsep Linear Programming (LP) adalah metode untuk menentukan alokasi yang optimal atas sumber daya langka yang melibatkan one objective dan multiple limiting factors.

Faktor restriksi dalam pencapaian suatu tujuan (objective) meliputi:

·         The physical constraint yang berhubungan dengan ukuran dari fasilitas tertentu

·         Ukuran dari pekerja (worker)

·         Labor hours the worker is allowed to work

·         Ketersediaan dana

B.       KONSEP DASAR OBJECTIVE, CONSTRAINT, AND ITS FUNCTION

1.        Objective (Tujuan)

Tujuan perusahaan dapat berupa maximize or minimize some measure of performance, seperti memaksimalkan contribution margin atau meminimalkan product cost.

2.        Constraint (Batasan atau Restriksi)

Merupakan hambatan manajemen dalam pencapaian tujuan. Dapat berupa resource constraints (production capacity, availability of labor time, space, raw material, dll) atau berupa demand or marketing constraints (quantity sold during time period).

3.        Function or Formulatting an LP Problem

Yang terpenting sejak awal : buat bentuk persamaan matematika dari data yang diberikan.

Untuk mengkonversi data informasi menjadi persamaan matematika, dibutuhkan decision variable yaitu elemen seperti number of units yang digunakan untuk menyelesaikan suatu masalah. Fungsi objektif dan constraint harus diidentifikasi.

Step 1 : Tentukan persamaan matematika dari suatu tujuan (objective function)

Basic Objective Function

Maximazation problems           Max CM =  CM₁X₁ + CM₂X₂

Minimazation problems            Min VC   =  VC₁X₁ + VC₂X₂

Ket :

CM = Contribution Margin                            CM_{1 atau 2} = CM per unit produk 1 atau 2

VC = Variable Cost                                           VC_{1 atau 2} = VC per unit produk 1 atau 2

X₁ = produk pertama

X₂ = produk kedua

  

Step 2 : Tentukan persamaan matematika dari suatu batasan (constraint)

Biasanya batasan sumber daya dinyatakan secara inequalities (tidak =)

Resource Constraint (1) = A₁X₁ + A₂X₂  ≤  Resource 1

Koefisien A1 dan A2 adalah koefisien input-output yang mengindikasikan setiap variable keputusan menggunakan atau menghabiskan sumber daya yang langka.

Step 3 : Membuat grafik constraint dan menentukan feasible region atau ruang grafik yang terisi semua garis constraint

Step 4 : Tentukan titik koordinat tiap corner (vetex) dari feasible region

Step 5 : Htung nilai objective function semua titik koordinat lalu pilih optimal soultion (max or min problems)

Jadi, Linear Programming ini bisa digunakan untuk memaksimalkan keuntungan dan meminimalisir biaya.

C.       MEMAKSIMALKAN CONTRIBUTION MARGIN

Contribution Margin (CM) sering menjadi acuan untuk melihat performa dari perusahaan. Untuk memperbesar keuntungan, maka perusahaan harus memperbesar contribution margin atau memperkecil biaya.

Berikut adalah contoh linear programming untuk memperbesar contribution margin :

Diasumsikan sebuah kedai kopi membuat 2 model produk, yaitu model standar dan deluxe.

·      Setiap unit model standar memerlukan waktu 2 jam untuk penggilingan dan 4 jam untuk pemolesan

·     Setiap unit model deluxe memerlukan waktu 5 jam untuk penggilingan dan 2 jam untuk pemolesan

·     Perusahaan memiliki 3 mesin penggilingan dan 2 mesin pemolesan

·    Setiap 40 jam waktu kerja mingguan menyediakan 120 jam kapasitas penggilingan dan dan 80 jam    kapasitas pemolesan

·    Model standar dijual dengan harga $9 dan model deluxe dijual dengan harga $12

·    Variable costs untuk membuat dan menjual per satu unit model adalah $6 untuk model standar dan      $8 untuk model deluxe

·     

      Akibatnya CM dari model standar adalah $3 dan model deluxe adalah $4

Informasi yang relevan adalaha sebagai berikut:

	Waktu Penggilingan	Waktu Pemolesan	Harga jual	Variable Cost	CM
Standard  model	2	4	$9	$6	$3
Deluxe model	5	2	12	8	4
Plant capacity	120	80

Persamaan matematikanya adalah:

1)   Objective function à maximize CM = 3x + 4y

2)   Constraint à waktu penggilingan à 2x +5y ≤ 120

                         Waktu pemolesan à 4x + 2y ≤ 80

Batasan à Waktu penggilingan = 2x + 5y ≤ 120

                    Waktu pemolesan = 4x + 2y ≤ 80

·         Dari persamaan batasan waktu penggilingan dan pemolesan, maka akan diperoleh:

2x + 5y = 120   x 2       4x + 10y = 240

4x + 2y = 80     x 1        4x +   2y =   80

                                              8y  = 160

                                                y = 160/8 = 20

                                                x = 10

lalu masukan ke fungsi objektifitas:

Maximize CM = 3x + 4y

                        = 3(10) + 4(20)

                        = 110

·         Dapat juga menggunakan cara grafik dengan menentukan feasible areanya

(1)        2x + 5y = 120

            x = 0 à y = 24

            y = 0 à x = 60

(2)        4x + 2y = 80

            x = 0 à y = 40

            y = 0 à x = 20

Berikut adalah gambar grafiknya :

 Setelah kita mendapatkan beberapa titik di grafik di atas, kita tinggal memasukkan setiap titik pada grafik tersebut ke dalam fungsi objektif, sehingga diperoleh :

·          (10,20)             Maximize CM = 3(10) x 4(20)  = 110 à CM paling tinggi

·          (0,24)               Maximize CM = 3(0) x 4(24)    = 96                                   

·          (20,0)               Maximize CM = 3(20) x 4(0)    = 60

Jadi, titik paling maksimal adalah titik x = 10 dan y = 20 yang dapat menghasilkan contribution margin sebesar 110.

D.    MEMINIMALISIR BIAYA

Berikut adalah contoh penggunaan linear programming untuk meminimalissir biayv :

     Diasumsikan terdapat perusahaan farmasi yang berencana untuk memproduksi tepatnya 40 galon yang terdiri dari campuran 2 bahan yaitu bahan x dan y yang memiliki biaya secara berurutan $8 dan $15 per galon. Tidak lebih dari 12 galon bahan x yang dapat digunakan, sedangkan untuk memastikan kualitas, minimal 10 galon bahan y harus digunakan. Perusahaan ingin meminimalisir biaya yang ditimbulkan.

Maka persamaan matematikanya adalah:

                 1)      Objective function à minimize cost = 8x + 15y

                 2)      Constraint à x + y = 40

                        x ≤ 12

                        y ≥ 10

Di kasus ini, kita harus mengoptimalkan penggunaan bahan x karena biayanya lebih murah dibandingkan bahan y. Sehingga jika kita mengoptimalkan bahan x, maka bahan x yang digunakan sebanyak 12 galon. Sedangkan sisanya adalah bahan y, yaitu sebanyak 28 galon (40-12).

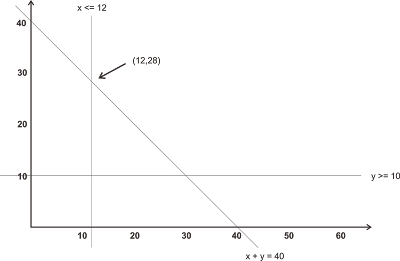
Jika diaplikasikan ke dalam sebuah grafik, hasilnya akan menjadi seperti ini :

Dari grafik di atas, bisa ditemukan dua titik. Kemudian masukkan kedua titik tersebut ke dalam fungsi objektif (objective function) :

·         (0,40)         Minimize cost = 8(0) + 15(40) = 600

·         (12,28)       Minimize cost = 8(12) + 15(28) = 516  à cost paling rendah

Maka, untuk meminimalkan biaya, bahan x digunakan sebanyak 12 galon, sedangkan bahan y sebanyak 28 galon.